Resumão Matemática #PARTIUENEM
- Uyara

- 19 de nov. de 2022
- 2 min de leitura
Abaixo um resumão dos principais temas abordados no ENEM e que você pode usar como guia nessas horas de revisão final.
A prova de matemática normalmente é a que gera mais medo nos alunos, mas na verdade é um conteúdo simples de se conhecer, se preocupe em entender o conceito, e assim você consegue desenvolver as fórmulas sem precisar de muito decoreba.
Vamos ao resumo?
Progressão arimética é uma sequência numérica em que a diferença entre um termo e seu antecessor resulta sempre em um mesmo valor, chamado de razão. Por exemplo, considere a sequência a seguir: (2, 4, 6, 8, 10, 12, 14, 16, 18, 20...) Podemos então dizer que a razão (r) dessa sequência numérica é 2.
De acordo com o valor da razão, as progressões aritméticas são classificadas em:
- Constante: quando a razão for igual a zero. Por exemplo: (4, 4, 4, 4, 4...), sendo r = 0.
- Crescente: quando a razão for maior que zero. Por exemplo: (2, 4, 6, 8,10...), sendo r = 2.
- Decrescente: quando a razão for menor que zero (15, 10, 5, 0, - 5,...), sendo r = - 5
1ª propriedade: Em uma P.A. finita, a soma de dois termos equidistantes dos extremos é igual à soma dos extremos.
2ª propriedade: Considerando três termos consecutivos de uma P.A., o termo do meio será igual a média aritmética dos outros dois termos.
3ª propriedade: Em uma P.A. finita com número de termos ímpar, o termo central será igual a média aritmética entre termos equidistantes deste. Esta propriedade deriva da primeira.
Fórmula do Termo Geral (PA)
an = a1 + (n-1).r
onde:
an: termo que queremos calcular a1: primeiro termo da P.A. n: posição do termo que queremos descobrir r: razão
Progressão Geométrica
Uma progressão geométrica (PG) é uma sequência numérica onde cada termo é igual ao produto de seu antecessor com uma constante, chamada razão da PG. Em outras palavras, a diferença entre dois termos quaisquer e consecutivos de uma PG é uma constante. Exemplo de progressão geométrica: (1, 3, 9, 27, 81, …)
De acordo com o valor da razão (q), podemos dividir as Progressões Geométricas (PG) em 4 tipos: PG Crescente. Na PG crescente a razão é sempre positiva (q > 0) formada por números crescentes, por exemplo: ... PG Decrescente. ... PG Oscilante. ... PG Constante.
Fórmula do Termo Geral (PG)
an = a1 . q(n-1)
onde:
an: número que queremos obter a1: o primeiro número da sequência q(n-1): razão elevada ao número que queremos obter, menos 1
Conjuntos
O estudo de conjuntos faz parte da base da Matemática e por isso é necessário que admitamos como existentes os conceitos primitivos.


Relaçõs entre elementos de um conjunto:
- Pertinência
- Continência
- Conjunto vazio
- Conjunto Universo
- Igualdade de conjuntos
Operações entre conjuntos
- União
- Interseção
- Complementar
- Diferença
- Conjunto das partes
- Número de elementos da união de conjuntos
Análise Combinatória

Probabilidade

Geometrica Plana


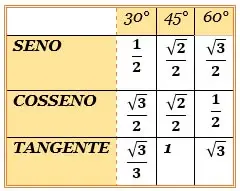
Trigonometria












Comentários